Durante siglos, la geometría euclidiana ha sido la base para comprender el mundo. Esta rama de las matemáticas, desarrollada en la antigua Grecia, describe formas simples y perfectas como líneas rectas, círculos, cubos y esferas. Sin embargo, cuando observamos la naturaleza, nos damos cuenta de que rara vez encontramos estructuras tan ordenadas.
En lugar de líneas rectas, vemos ramas irregulares en los árboles; en lugar de círculos perfectos, encontramos formas ondulantes en las costas y nubes. Aquí es donde entra en juego la geometría fractal, una herramienta matemática que nos permite entender la complejidad del mundo natural.

La geometría euclidiana y sus limitaciones
La geometría euclidiana, basada en axiomas y teoremas formulados por Euclides en el siglo III a.C., nos ha permitido modelar el mundo en términos de formas regulares y proporciones exactas. Su aplicación es fundamental en arquitectura, ingeniería y muchas disciplinas científicas. Sin embargo, al intentar describir elementos naturales como montañas, nubes, sistemas vasculares o la distribución de galaxias, nos encontramos con sus limitaciones:
- No representa la irregularidad: Las montañas no son conos perfectos, los árboles no tienen cilindros exactos y los ríos no fluyen en líneas rectas.
- No permite escalas múltiples: En la geometría euclidiana, los objetos tienen una dimensión fija (1D, 2D o 3D), mientras que en la naturaleza, las estructuras pueden repetirse a distintas escalas.
- No explica el caos aparente: La naturaleza parece seguir un orden dentro del desorden, algo que la geometría tradicional no puede modelar con precisión.
La geometría fractal: el lenguaje de la naturaleza
En 1975, el matemático Benoit Mandelbrot revolucionó la manera en que entendemos la naturaleza con la introducción de la geometría fractal. Los fractales son patrones que se repiten a diferentes escalas, es decir, una misma estructura se replica en sus partes más pequeñas. Esto permite modelar formas que antes parecían caóticas e impredecibles.
Ejemplos de fractales en la naturaleza
Los fractales están en todas partes. Algunos ejemplos incluyen:
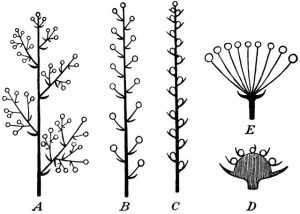
- Árboles y plantas: La forma en que las ramas se dividen en un árbol sigue un patrón fractal, repitiéndose a diferentes escalas desde el tronco hasta las hojas.
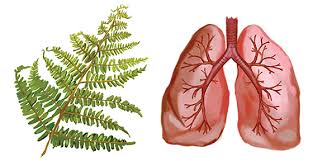
Sistemas circulatorios y respiratorios: Los vasos sanguíneos y los bronquios se ramifican de la misma manera que los árboles, optimizando la distribución de nutrientes y oxígeno.
- Ríos y costas: La manera en que los afluentes de un río se dividen y el contorno irregular de una costa siguen patrones fractales.
- Pulmones y neuronas: La estructura del pulmón humano y las conexiones neuronales también presentan organización fractal, maximizando su eficiencia en un espacio reducido.
Rayos y tormentas: La forma en que un rayo se expande en el cielo o la estructura de una tormenta siguen patrones fractales.

¿Por qué la naturaleza usa fractales?
La geometría fractal no solo es una curiosidad matemática, sino que representa un principio fundamental en la organización del universo. Algunas razones por las cuales la naturaleza sigue estos patrones incluyen:
- Eficiencia energética: Los fractales permiten maximizar la superficie en un espacio reducido, como en los pulmones o en las raíces de las plantas.
- Optimización del crecimiento: Las estructuras fractales permiten que los organismos crezcan siguiendo principios simples, repitiendo patrones sin necesidad de información adicional.
- Adaptabilidad: La capacidad de replicar estructuras a diferentes escalas permite a los organismos responder mejor a su entorno.
Conclusión: la geometría de la vida
La geometría euclidiana ha sido una herramienta poderosa para la ciencia y la ingeniería, pero no es suficiente para describir la complejidad de la naturaleza. La geometría fractal nos permite entender los patrones ocultos en el mundo natural, revelando que el aparente caos sigue reglas precisas.
Desde la forma de una nube hasta el crecimiento de una neurona, todo en la naturaleza parece seguir este principio fractal, demostrando que la vida misma es un juego de patrones repetitivos a distintas escalas.
Con esta perspectiva, podemos apreciar que la naturaleza no es solo belleza y caos, sino un sofisticado diseño matemático que apenas estamos comenzando a comprender.